Einschreiben mit stexana
- Учитель: Heribert Zenk
- Учитель: Sebastian Hensel
- Учитель: Jose Rodriguez Migueles
Riemannian Geometry is the study of manifolds with a Riemannian metric. In this course, we will begin by discussing basic geometric objects (geodesics, Jacobi fields, curvature). Particular emphasis will be given to geometric interpretation and intuition behind the (analytic) objects of differential geometry, and how to use the analysis to answer geometric questions.
Once the basic notions have been covered, the course will discuss connections between geometry and topology of manifolds, and comparison geometry. The latter allows to interpret curvature bounds in a purely metric fashion, and leads towards metric geometry and geometric group theory.
Prerequisites: Differentiable manifolds (including vector bundles and linear connections). Some topology is helpful, but not necessary.
Suitable for: Masters students in mathematics, TMP students
Time and date: The lecture takes place Tuesday/Thursday 10-12 in room A027. There is a problem session which takes place Wednesday 10-12 in room A027 (starting in week 2 of the semester)- Учитель: Sebastian Hensel
Einschreibeschlüssel: Diff2SS23
- Учитель: Sonja Fischl
- Учитель: Anna Ribelles Perez
- Учитель: Daniel Rost
Einschreibeschlüssel: LA2SS23
- Учитель: Matija Pasch
- Учитель: Daniel Rost
Einschreibeschlüssel: Querschnitt23S
- Учитель: Erwin Schörner
- Учитель: Alois Wohlschlager
Einschreibeschlüssel: Grundlagen2S23
- Учитель: Lukas Böke
- Учитель: Erwin Schörner
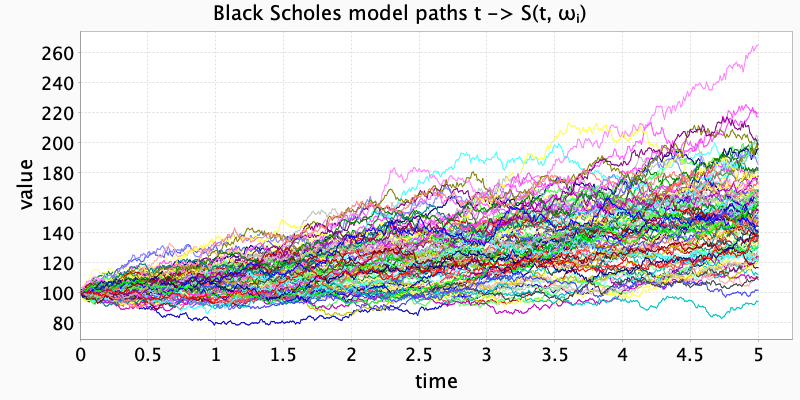
This lecture introduces into the arbitrage theory of fixed income markets and interest rate/credit derivatives. Topics that are covered include
- Introduction to interest rates and interest rate derivatives: bonds, various interest rates, swaps, caps, floors, swaptions, market conventions
- Arbitrage pricing: portfolios, arbitrage, hedging valuation.
- Short-rate models
- Affine term structure models
- HJM models
- Forward measures
- LIBOR market models
- Credit risk and Related Contracts
- Structural Models
- Reduced-Form Models
Main reference:
- Filipovic: Term-Structure Models: A Graduate Course, Springer.
Additional literature:
- Andersen and Piterbarg: Interest rate modelling, Volume 1,2,3, Atlantic Financial Press.
- Björk: Arbitrage Theory in Continuous Time, Oxford University Press.
- Brigo and Mercurio: Interest rate models-Theory and practice: With Smile, Inflation and Credit, Springer.
- Lando: Credit Risk Modelling: Theory and Applications, Princeton Series in Finance.
- Учитель: Karl-Wilhelm Georg Bollweg
- Учитель: Thilo Meyer-Brandis
- Учитель: Annika Steibel
Einschreibeschlüssel: WTH
- Учитель: Alexander Kalinin
- Учитель: Franz Merkl
Einschreibeschlüssel: ExamUF23S
- Учитель: Daniel Rost
- Учитель: Erwin Schörner
Inhalt: Viele von den Dingen die im Zyklus Algebraische Topologie unter den Tisch fallen, z.B. Konstruktion stetiger Funktionen, Metrisierbarkeit, uniforme Räme, etc.
Zielgruppe: Bachelor/Master Mathematik. Vom Niveau irgendwo zwischen dem vierten und sechsten Semester. Lehramtsstudenten sind willkommen, ich weise aber darauf hin dass diese Vorlesung die GTF-Vorlesung nicht ersetzt.
Einschreibeschlüssel: Pavel
- Учитель: Lukas Böke
- Учитель: Thomas Vogel
- Учитель: Christian Fries
- Учитель: Andrea Mazzon
- Учитель: Niklas Weber
Dies ist der zweite Teil der Mathematik Vorlesungen im Bachelor Physik. Wir starten am Dienstag 18. April 2023 um 8.30 Uhr im C123. Zuerst werden wir mit Linearer Algebra (weiter-)machen. Die (Zentral-)Übung startet am Mittwoch 19. April 2023 um 16.15 Uhr im C123 mit einer zusätzlichen Vorlesung.
Einschreibung mit Passwort ALAIIP
- Учитель: Heribert Zenk
- Bachelor Mathematik (Modul WP17, PO 2021 bzw. Modul WP6, PO 2015)
- Bachelor Wirtschaftsmathematik (Modul P12)
- LA Gymnasium (Modul P6, PO 2021 bzw. Modul P6, PO 2011 anstelle von "Funktionentheorie, Lebesguetheorie und gewöhnliche Differentialgleichungen")
- Учитель: Rupert Frank
- Учитель: Jonas Peteranderl
- Учитель: Jakob Stern
- Учитель: Leonard Wetzel
In dieser Vorlesung wird die Einführung in die Lineare Algebra vom ersten Semester fortgeführt. Zusammen mit der Linearen Algebra I ist diese Vorlesung unverzichtbare Grundlage für nahezu alle weiterführenden Veranstaltungen der Mathematik. Wichtige Themen und Inhalte sind unter anderem: Bilineare Abbildungen, euklidische und unitäre Vektorräume, Hauptachsentransformation und Normalformen von Matrizen. Dies wird ergänzt durch eine Auswahl aus folgenden Themen: euklidische Ringe, Moduln über euklidischen Ringen oder Hauptidealringen, Elemente der elementaren Zahlentheorie oder einfache Anwendungen in der Kryptographie.
Einschreibeschlüssel: cayley-hamilton
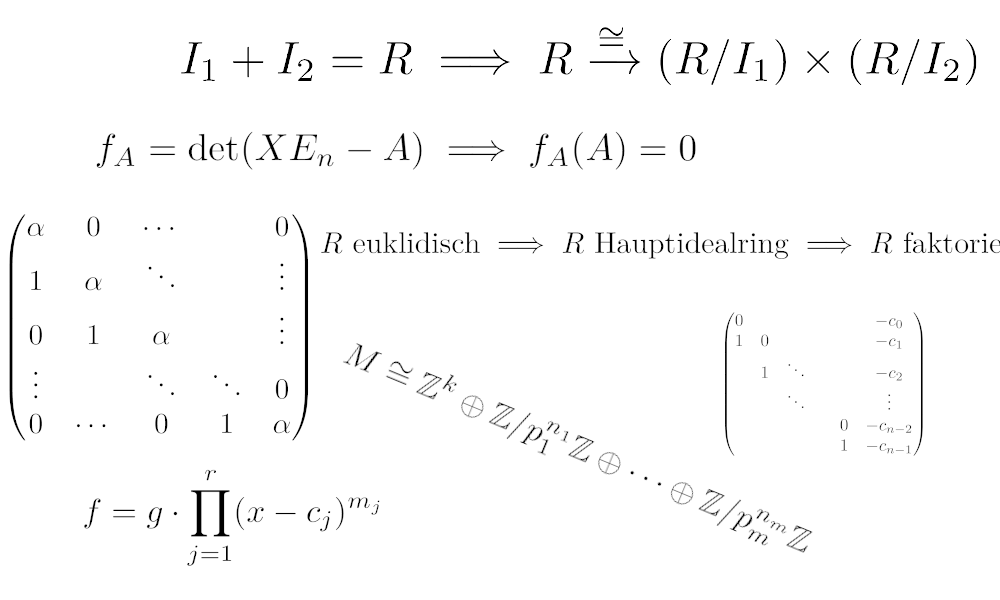
- Учитель: Werner Bley
- Учитель: Andrei Lavrenov
- Учитель: Panagiotis Papadopoulos
- Учитель: Simon Weinzierl
- Учитель: Matthias Bauernfeind
- Учитель: Simone Rademacher
- Учитель: Markus Land
- Учитель: Robin Mader
- Учитель: Maksim Zhykhovich
Description
The overall subject is Many-body Quantum mechanics. We will start with atoms and molecules and prove the famous theorem on stability of matter, which says that the energy of a system with N electrons and M nulclei can bounded from below by -C(N+M). Subsequently we show the existence of the thermodynamic limit of Coulomb systems. Next we study bosonic systems, recall the original argument of Bose and Einstein, and then prove Bose-Einstein-Condensation for interacting systems. Next, we study fermionic systems modeling metals and describe the Hartree-Fock approximation, followed by studying the correlation energy, including recent results. Finally we consider the mathematical properties of the BCS theory of superconductivity, and compare with results from the physics literature.
Please note: MQM1 is NOT a prerequisite!
Enrolement key: mqm2_2023@lmu
- Учитель: Emanuela Giacomelli
- Учитель: Christian Hainzl
- Учитель: Oliver Cooley
- Учитель: Umberto De Ambroggio
- Учитель: Tamas Makai
- Учитель: Konstantinos Panagiotou
This class is meant for everyone interested in problem solving, ML or quant finance 🧐💻 If you want to participate feel free to text us via walter@math.lmu.de or weber@math.lmu.de.
The registration key is beyondtheobvious.
Organization:
Our first meeting will take place on 20th April from 16-18 o'clock in room B251 (Mathematical Institute)
Target Group:
- BSc students of (business) mathematics with good knowledge of stochastic and preferably probability theory
- MSc students of (financial) mathematics
Although the class is mainly tailored for mathematics students, all students from quantitative subjects (e.g. physics, computer science, statistics) are very welcomed to join!
Content:
The content of the class can be structured in three pillars:
- Brainteasers and Logic Problems
- Coding Problems
- Useful and Interesting Theory
- Учитель: Niklas Walter
- Учитель: Niklas Weber
Das Seminar richtet sich vornehmlich an Bachelorstudierende, Masterstudierende sind aber auch herzliche willkommen. Wir wollen uns anhand des Buches „Non-Life Insurance Mathematics“ von Thomas Mikosch grundlegende mathematische Modelle der Schadenversicherung erarbeiten. Stichworte hierzu sind:
- Schadenzahlprozesse
- Modelle für den Gesamtschaden eines Versicherungsportfolios
- Ruintheorie
- Bühlmann- und Bühlmann-Straub-Modelle
Interesse? Dann schreiben Sie mir bis zum 16.4.2023 eine E-Mail. Idealerweise verteilen wir dann in der ersten Seminarsitzung am 17.4.2023 bereits die Themen.
Zeit und Ort: Montags, 14-16 Uhr, Raum B 041.
Referenz:
Thomas Mikosch: Non-Life Insurance Mathematics: An Introduction with the Poisson Process.
Springer (2009), https://link.springer.com/book/10.1007/978-3-540-88233-6
Schlüssel: Versicherung
- Учитель: Felix-Benedikt Liebrich
- Учитель: Felix-Benedikt Liebrich
- Учитель: Niklas Walter
For all information (including the password), see the course webpage.
- Учитель: Thomas Sørensen
- Учитель: Alejandro Caicedo Serrano
- Учитель: Sabine Jansen
Time and Location
Tue 12 - 14 in B005, Thu 10 - 12 in B004
Synopsis
(Linear) Functional analysis can be viewed as "linear algebra on infinite-dimensional vector spaces".
As such it is a merger of analysis and linear algebra. The concepts and results of functional analysis are important to a number of other mathematical disciplines, e.g., numerical mathematics, approximation theory, partial differential equations, and also to stochastics; not to mention that the mathematical foundations of quantum physics rely entirely on functional analysis. This course will present the standard introductory material to functional analysis: topological foundations, Banach and Hilbert spaces, dual spaces, Hahn-Banach thm., Baire thm., open mapping thm., closed graph thm., weak topologies. If time permits we will also cover Fredholm theory for compact operators and the spectral theorem.
Prerequisites
Audience
Literature
- M Reed and B Simon, Methods of modern Mathematical Physics I: Functional analysis, Academic Press, 1980
[excellent textbook with a focus on spectral theory, beginning not very gentle, proofs sometimes a bit brief; unfortunately rather pricey] - D Werner, Einführung in die Funktionalanalysis, Springer, 2007
[a German classic, covers a broad range of topics, including historical remarks] - M Dobrowolski, Angewandte Funktionalanalysis, Springer, 2006
[the basics of functional analysis plus a thorough discussion of Sobolev spaces and elliptic PDE's] - E Kreyszig, Introductory functional analysis with applications, Wiley, 1978
[thorough and pedagogical, very explicit proofs, does not cover all topics treated in the course (e.g. no Lp-spaces)] - P D Lax, Functional Analysis, Wiley, 2002
[well readable with an emphasis on spectral theory and some applications to quantum mechanics] - F Hirzebruch and W Scharlau, Einführung in die Funktionalanalysis, BI Mannheim, 1971
[another German classic, elegant but very(!) concise]
Enrolement Key
Hilbert&Co23 (valid from 1 April until 31 May 2023)- Dozent / Assistent: Leon Bollmann
- Dozent / Assistent: Peter Müller
- Учитель: Christian Lange
- Учитель: Bernhard Leeb