- Teacher: Andreas Leckner
- Teacher: Korbinian Meindl
- Teacher: Katharina Oberpriller
- Teacher: Leonardo Galli
- Teacher: Holger Rauhut
- Teacher: Shan Wei
- Teacher: Dirk Deckert
- Teacher: Kaan Savas
- Teacher: Anna Warlimont
- Teacher: Dieter Kotschick
- Teacher: Jonas Stelzig
- Teacher: Simon Gritschacher
- Teacher: Thomas Vogel
- Teacher: Alois Wohlschlager
- Teacher: Maksim Zhykhovich
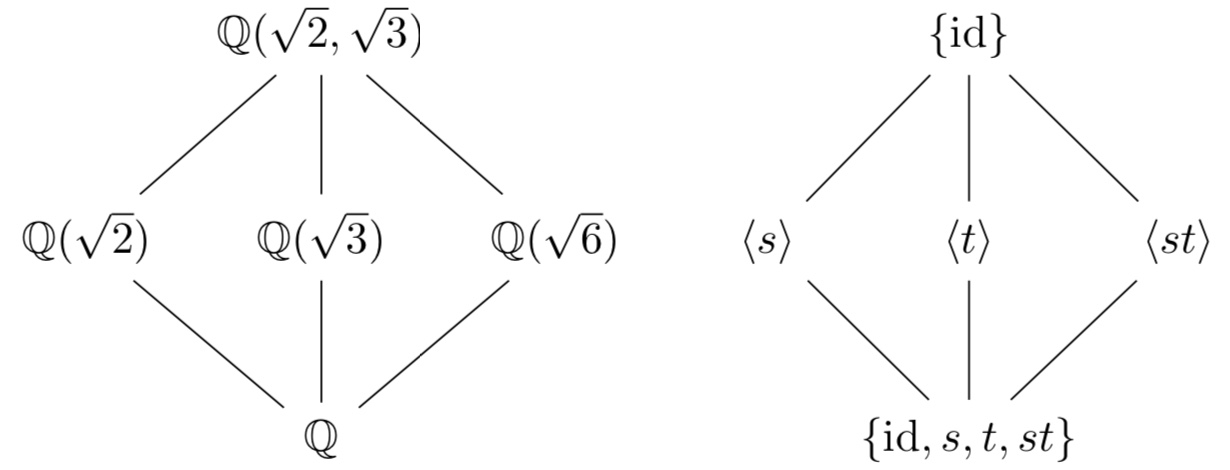
Die Vorlesung gibt eine Einführung in die Theorie fundamentaler algebraischer Strukturen. Unter anderem behandeln wir elementare Gruppentheorie, Gruppenoperationen, die Sylow-Sätze, Ringtheorie, insbesondere Teilbarkeit, Ideale und Polynomringe, sowie Körpererweiterungen und Galoistheorie. Als Anwendung beweisen wir, dass für Polynome vom Grad >= 5 keine allgemeine Lösungsformel existiert.
- Teacher: Andreas Rosenschon
- Teacher: Simon Seidenschwarz
Klausuranmeldung (29.01. - 05.02.2024) ausschließlich über Moodle.
- Teacher: Leon Bollmann
- Teacher: Florian Haberberger
- Teacher: Thomas Sørensen
Einschreibeschlüssel: AnIS2324
- Teacher: Sakirudeen Abdulsalaam
- Teacher: Oliver Cooley
- Teacher: Lukas Emmert
- Teacher: Daniel Misselbeck-Wessel
- Teacher: Peter Philip
- Teacher: Christian Lange
- Teacher: Bernhard Leeb
das ist die Vorlesung für Mathematik Lehramt Gymnasium im ersten Semester.
Einschreibung mit Einschreibeschlüssel ALAI
- Teacher: Matthias Bauernfeind
- Teacher: Morena Maierbacher
- Teacher: Kajetan Söhnen
- Teacher: Heribert Zenk
- Teacher: Adalbert Fono
- Teacher: Gitta Kutyniok
- Teacher: Ernesto Araya Valdivia
- Teacher: Katharina Bieker
- Teacher: Mariia Seleznova
- Teacher: Laura Thesing
Einschreibeschlüssel: DiffInt1W23
- Teacher: Erwin Schörner
- Teacher: Leonard Wetzel
Einführung in Finanzmathematik in diskreter Zeit.
Einschreibeschlüssel: fima1
- Teacher: Karl-Wilhelm Georg Bollweg
- Teacher: Katharina Oberpriller
The lecture provides an introduction to stochastic calculus with an emphasis on the mathematical concepts that are later used in the mathematical modeling of financial markets.
In the first part of the
lecture course the theory of stochastic integration with respect to
Brownian motion and Ito processes is developed. Important results such
as Girsanov's theorem and the martingale representation theorem are also
covered. The first part concludes with a chapter on the existence and
uniqueness of strong and weak solutions of stochastic differential
equations.
The second part of the lecture course gives an introduction to the arbitrage theory of financial markets in continuous time driven by Brownian motion. Key concepts are the absence of arbitrage, market completeness, and the risk neutral pricing and hedging of contingent claims. Particular attention will be given to the the Black-Scholes model and the famous Black-Scholes formula for pricing call and put options.
If you wish to participate in the
course, please sign up by sending an e-mail from
your LMU e-mail address to Annika Steibel (steibel@math.lmu.de).
- Teacher: Karl-Wilhelm Georg Bollweg
- Teacher: Thilo Meyer-Brandis
- Teacher: Annika Steibel
In this course we will use classical tools in harmonic analysis to study nonlinear differential equations. In the first part, we will discuss some popular evolution equations such as heat equations, wave equations and Schrödinger equations where basic Fourier analysis tools are helpful. In the second part, we will focus on concrete models coming from fluid mechanics (e.g. Navier–Stokes and Euler equations) for which the Littlewood- Paley decomposition plays a prominent role.
The course is suitable for master students and motivated bachelor students. Prerequisites: Lebesgue integration and L^2 theory of the Fourier transform. Knowing some basic results from harmonic analysis (e.g. Maximal inequalities, Littlewood–Paley theory, ...) are helpful, but not mandatory since they will be recalled properly.
Course homepage: https://www.math.lmu.de/~nam/Fourier2324.php
- Teacher: Thành Nam Phan
- Teacher: Martin Christiansen
- Teacher: Christian Hainzl
Einschreibeschlüssel: Grund1WS23
- Teacher: Lukas Böke
- Teacher: Daniel Rost
- Teacher: Stefan Kolek Martinez de Azagra
- Teacher: Johannes Maly
Einschreibeschlüssel: ExamUF23W
- Teacher: Daniel Rost
- Teacher: Erwin Schörner
Einschreibeschlüssel: LinAlg1W23
- Teacher: Oliver Hendrichs
- Teacher: Erwin Schörner
Registration code: mqm23
Description:
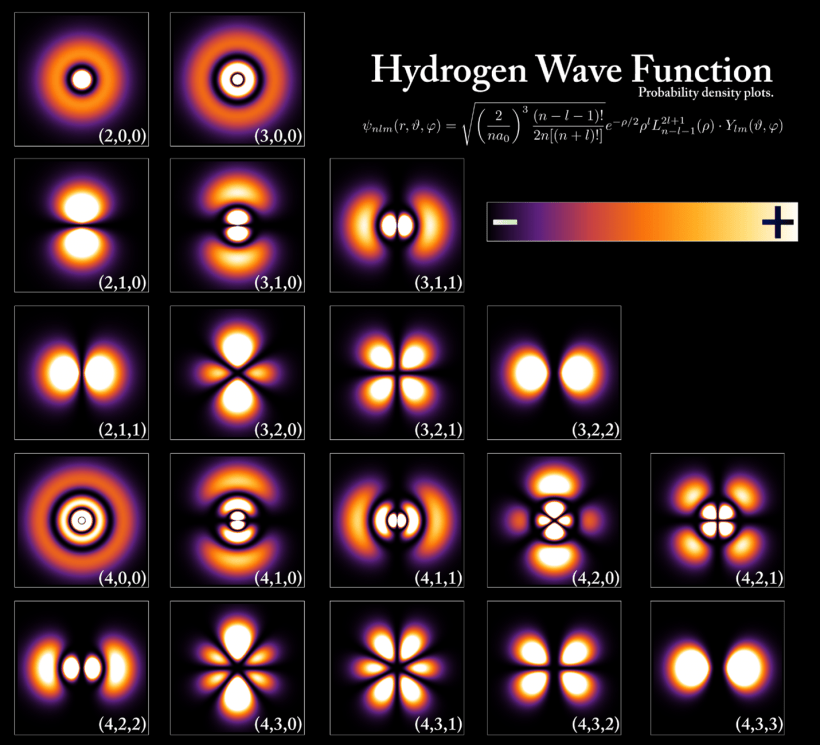
In this course we present the basic and fundamental mathematical tools allowing to formulate and use quantum mechanics. In its early days, quantum mechanics have seen two mathematical apparatus competing to formalize it: Heisenberg's matrix mechanics and Schrödinger's wave mechanics. As we will see, these two pictures are in fact equivalent and can be unified using the tools of spectral theory, functional analysis, harmonic analysis, etc.
- Teacher: Emanuela Giacomelli
- Teacher: Armin Scrinzi
- Teacher: Arnaud Triay-Alcouffe
- Teacher: Julian Becker
- Teacher: Lea Boßmann
- Teacher: Tamas Makai
- Teacher: Konstantinos Panagiotou
- Teacher: Anna Ribelles Perez
- Teacher: Fotios Siammenos
Mathematik I für Physiker
Einschreibeschlüssel: 23WSM1
- Teacher: Dirk Deckert
- Teacher: Jago Silberbauer
Dies ist der dritte Teil des Einführungskurses in Mathematik für das Physikstudium. Einschreibung mit Einschreibeschlüssel MIIIP
- Teacher: Matthias Bauernfeind
- Teacher: Christoph Mittermaier
- Teacher: Panagiotis Papadopoulos
- Teacher: Heribert Zenk
Einschreibeschlüssel: MiQWS23
- Teacher: Daniel Rost
Einschreibeschlüssel: Num2324
- Teacher: Charlotte Dietze
- Teacher: Peter Philip
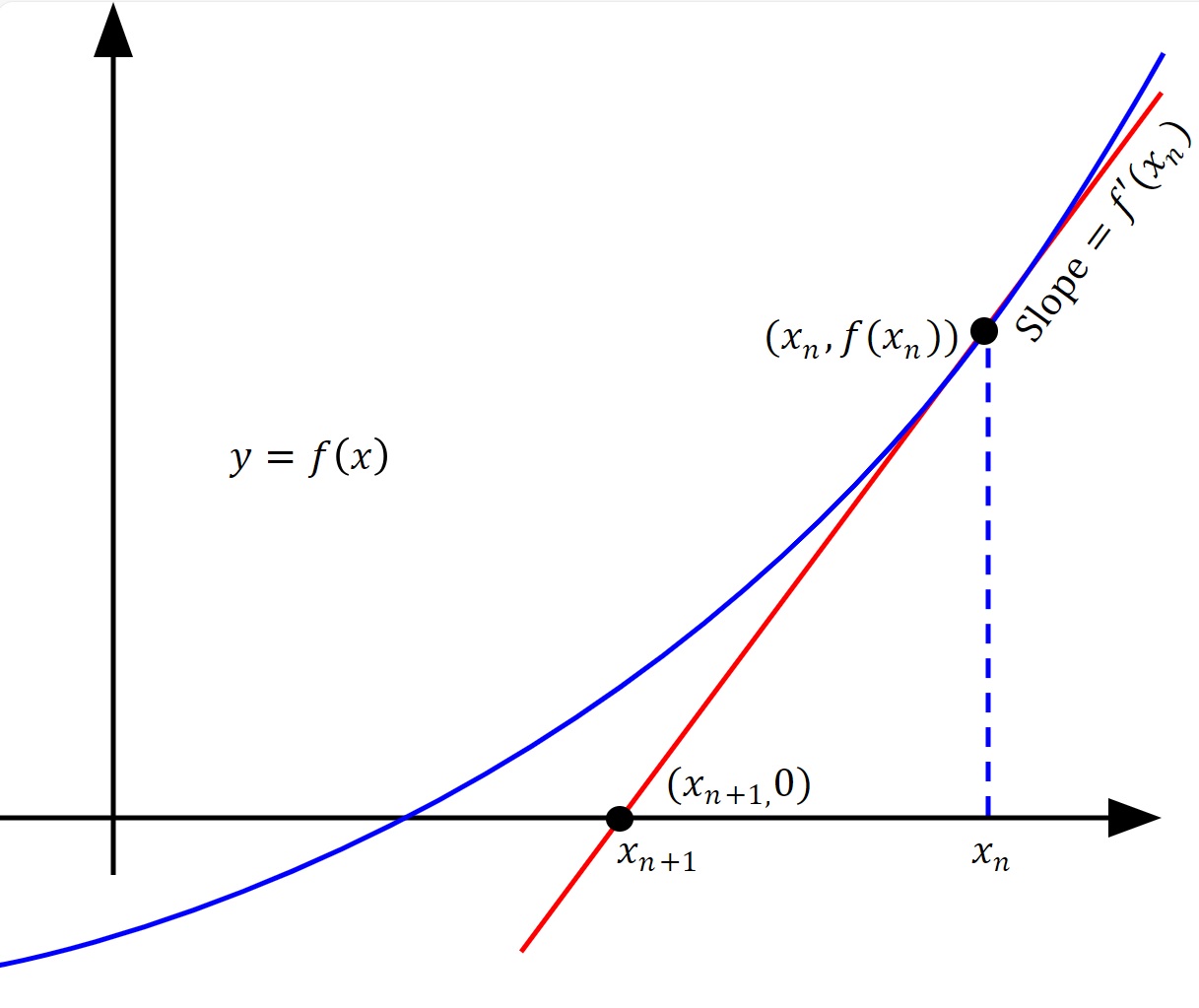
Inhalt der Vorlesung ist eine Einführung in die Optimierung in - vornehmlich - endlicher Dimension. Wichtige Themen und Inhalte sind unter anderem:
Lineare Programme und ihre Standardformen, Existenz von Lösungen für lineare Programme, Dualitätstheorie für lineare Programme, das Simplexverfahren, Formulierung und Existenz von Lösungen konvexer Optimierungsprobleme, duale Darstellung konvexer Funktionen und die Kuhn-Tucker-Theorie.
- Teacher: Julian Becker
- Teacher: Ari-Pekka Perkkiö
Registration key: PDE1
- Teacher: Vincent Ariksoy
- Teacher: Lukas Emmert
- Teacher: Rupert Frank
- Teacher: Jakob Stern
- Teacher: Werner Bley
- Teacher: Eva Brenner
This class is meant for everyone interested in problem solving, ML or quant finance 🧐💻 If you want to participate feel free to text us via walter@math.lmu.de or weber@math.lmu.de.
The registration key is beyondtheobvious.
Organization:
Our first meeting will take place on 19th October from 16-18 o'clock in room B251 (Mathematical Institute)
Target Group:
Advanced BSc and MSc students in mathematics, physics, computer science, statistics and similar quantitative subjects
Content:
The content of the class can be structured in three pillars:
- Brainteasers and Logic Problems
- Coding Problems
- Useful and Interesting Theory

- Teacher: Niklas Walter
- Teacher: Niklas Weber
Course Description
In this lecture, we will consider various classes of stochastic processes that may differ in their state spaces and underlying index sets with a special focus on Gaussian, Lévy and Markov processes. In summary, the lecture will be divided into three core topics: the construction, the path behaviour and the probabilistic analysis of general stochastic processes.
- Master students of Mathematics and Financial and Insurance Mathematics
- Probability theory and measure and integration theory
- Processes
- Teacher: Alexander Kalinin
- Teacher: Sergey Aristarkhov
- Teacher: Simone Rademacher
- Teacher: Gitta Kutyniok
- Teacher: Mariia Seleznova
- Teacher: Simon Gritschacher
- Teacher: Markus Land
Einschreibeschlüssel stexana
- Teacher: Heribert Zenk
Einschreibeschlüssel: Distributionen
- Teacher: Heribert Zenk