- Profesor: Fabian Darabi Far
- Profesor: Marleen Fiederer
- Profesor: Boyan Kugiyski
- Profesor: Kajetan Söhnen
- Profesor: Katharina Wendler
- Profesor: Heribert Zenk
- Profesor: Umberto De Ambroggio
- Profesor: Tamas Makai
- Profesor: Konstantinos Panagiotou
- Profesor: Johannes Maly
- Profesor: Mariia Seleznova
- Profesor: Aras Bacho
Einschreibeschlüssel: DiffInt2S24
- Profesor: Erwin Schörner
- Profesor: Leonard Wetzel
Die Vorlesung behandelt grundlegende Fragestellungen aus der diskreten Mathematik, insbesondere aus der Kombinatorik und der Graphentheorie.
- Profesor: Julian Becker
- Profesor: Konstantinos Panagiotou
- Profesor: Johannes Bartenschlager
- Profesor: Lukas Böke
- Profesor: Jakob Neumaier
- Profesor: Panagiotis Papadopoulos
- Profesor: Thomas Vogel
- Profesor: Leon Vollmar
Course Description
Target Participants
- Master students of Financial and Insurance Mathematics and Mathematics
Pre-requisites
- Probability theory and foundations of stochastic processes in continuous time
Registration key
- SPDE
- Profesor: Alexander Kalinin
- Profesor: Thilo Meyer-Brandis
- Profesor: Annika Steibel
- Profesor: Emanuela Giacomelli
- Profesor: Christian Hainzl
- Profesor: Christian Lange
- Profesor: Bernhard Leeb
Einschreibeschlüssel: Grund2SS24
- Profesor: Lukas Böke
- Profesor: Laura Paul
- Profesor: Daniel Rost
- Profesor: Markus Land
- Profesor: Christoph Winges
Einschreibeschlüssel: ExamUF24S
- Profesor: Daniel Rost
- Profesor: Erwin Schörner
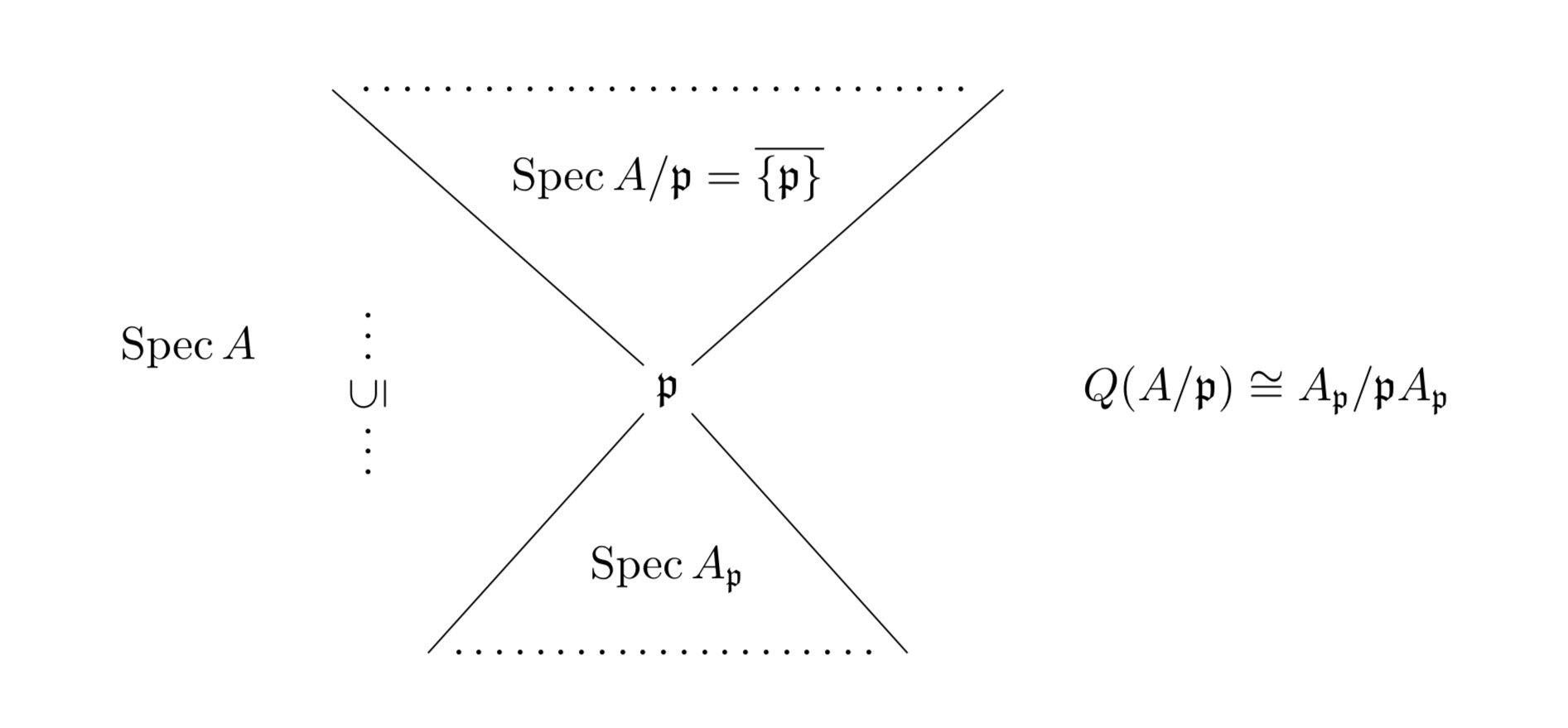
The lecture serves as an introduction to commutative algebra. We treat basic concepts such as prime ideals, dimension, localization and integrality, as well as modules over commutative rings. Additionally, we give an outlook on (affine) algebraic geometry and algebraic number theory.
- Profesor: Andreas Rosenschon
- Profesor: Simon Seidenschwarz
- Profesor: Simon Gritschacher
- Profesor: Thomas Vogel
Einschreibeschlüssel: LinAlg2S24
- Profesor: Oliver Hendrichs
- Profesor: Erwin Schörner
- Profesor: Leonardo Galli
- Profesor: Holger Rauhut
- Profesor: Peter Madsen
- Profesor: Arnaud Triay-Alcouffe
- Profesor: Alejandro Caicedo Serrano
- Profesor: Sabine Jansen
- Profesor: Armin Scrinzi
Für weitere Information verweisen wir auf https://www.ai.math.uni-muenchen.de/teaching/sose2024/math_dnns/index.html
- Profesor: Adalbert Fono
- Profesor: Gitta Kutyniok
- Profesor: Ernesto Araya Valdivia
- Profesor: Adalbert Fono
- Profesor: Gitta Kutyniok
Einschreibeschluessel: MiQSS24
- Profesor: Stefan Kolek Martinez De Azagra
- Profesor: Stefan Kolek Martinez de Azagra
- Profesor: Daniel Rost
Das Seminar "Mathematische und statistische Methoden (Pharmazie) startet
(wegen der Einführungsveranstaltungen) erst am Montag 22.4.2024 um 8.15
Uhr in B051, Theresienstraße 39.
Einschreibeschlüssel: msmph
- Profesor: Heribert Zenk
- Profesor: Christian Fries
- Profesor: Alessandro Sgarabottolo
- Profesor: Niklas Walter
- Profesor: Niklas Weber
Goal: The course will focus on finite element methods and the applications in partial differential equations. In particular, we will discuss the variational formulation of elliptic boundary value problem in Sobolev spaces, the construction of finite element spaces, finite element multigrid methods as well as Schwarz domain decomposition methods.
- Profesor: Thành Nam Phan
- Profesor: Rupert Frank
- Profesor: Larry Read

- Profesor: Niklas Walter
- Profesor: Niklas Weber
This course is an introduction into the theoretical concepts and modelling approaches of quantitative risk management.
The first part of the course covers various methods from probability and statistics to model market, credit and operational risk. This includes multivariate models, dimension reduction techniques, copulas and dependence modelling, risk aggregation, credibility and insurance risk theory. The second part of the lecture then focuses on portfolio allocation and stochastic optimal control.
- Profesor: Karl-Wilhelm Georg Bollweg
- Profesor: Katharina Oberpriller
Wir starten mit einem kurzen Überblick über verschiedene Typen und
Eigenschaften von -- in den meisten Fällen unbeschränkten -- Operatoren,
wie etwa abgeschlossene, symmetrische oder selbstadjungierte
Operatoren. Je nach Kenntnisstand der Teilnehmer werden wir den
Spektralsatz für einen selbstadjungierten Operator wiederholen oder
beweisen. Die Anwendungen des Spektralsatzes wie
- stark stetige unitäre einparametrige Gruppen und deren Generatoren
- stark kommutierende selbstadjungierte Operatoren
- Spektralsatz für stark kommutierende selbstadjungierte Operatoren
stehen dann im Mittelpunkt. Einschreibung mit Einschreibeschlüssel Selbst- Profesor: Heribert Zenk
The topics covered in these lectures are applications of functional analysis techniques to various areas of mathematics. In particular, we will focus on applications to quantum mechanics and the calculus of variations.
Enrolment key: STRFA
- Profesor: Emanuela Giacomelli
- Profesor: Christian Hainzl
Einschreibeschlüssel: Stochastik24
- Profesor: Tamas Makai
- Profesor: Quirin Vogel
- Profesor: Arthur Wachtel
- Profesor: Markus Land
- Profesor: Christoph Winges
Einschreibung schliesst am 1. Mai.
Klausuranmeldung (08.07. - 15.07.2024) ausschließlich über Moodle.
- Profesor: Leon Bollmann
- Profesor: Jonas Peteranderl
- Profesor: Thomas Sørensen
Wir werden typische Aufgabenstellungen beim Staatsexamen in Analysis behandeln,
Lösungsmethoden besprechen und evtl. noch etwas zugrunde liegende Theorie
wiederholen. Wir beginnen mit dem Themenbereich Funktionentheorie und
arbeiten uns dann zur reellen Analysis und den
gewöhnlichen Differentialgleichungen durch.
Wir starten am Mittwoch 17.4.2024 und Donnerstag 18.4.2024 mit
ganz "normalem" Aufgabenrechnen. Donnerstag 8.30-10 Uhr in B 006 (ab 25.4.)
besprechen wir den Ernstfalltest der letzten Woche. Donnerstag 10-12 Uhr in B006 (ab 25.4.) ist der Versuch, von allen gängigen Typen zumindest eine Aufgabe zu
rechnen. Mittwoch 10-12 Uhr in B006 (ab 24.4.)
werden wir zur Wiederholung und Beantwortung von Fragen nutzen.
Einschreiben mit Einschreibeschlüssel stex
- Profesor: Heribert Zenk
Einschreibeschlüssel auf der Webseite! Einschreibung erst ab 2. April!
- Profesor: Thomas Sørensen
- Profesor: Sebastian Hensel
- Profesor: Anna Ribelles Perez
- Profesor: Emre Yüksel
Einschreibeschlüssel: Wahrscheinlichkeitstheorie
- Profesor: Franz Merkl
- Profesor: Fabian Nolte