- Учитель: Christian Hainzl
- Учитель: Peter Madsen
- Учитель: Riccardo Panza
- Учитель: Leonardo Galli
- Учитель: Gabin Nguegnang
- Учитель: Holger Rauhut
- Учитель: Adalbert Fono
- Учитель: Ralf Gerkmann
- Учитель: Tamas Makai
This is a continuation of the lecture course Functional Analysis from the previous semester. Attendance of the latter is not a necessary prerequisite for this course. However, a background in the theory of Banach and Hilbert spaces will be required. Main topics to be covered are a proof of the spectral theorem for bounded self-adjoint operators, an introduction to unbounded symmetric and self-adjoint operators and the basics of the Fourier transform and distributions.
Einschreibeschlüssel: selbstadjungiert
- Учитель: Peter Müller
- Учитель: Leonard Wetzel
- Учитель: Lyn Assy
- Учитель: Jonas Beyrer
- Учитель: Marie Diesenberger
- Учитель: Johannes Heißler
- Учитель: Garam Kim
- Учитель: Franz Merkl
- Учитель: Arianna Rast
- Учитель: Benjamin Schoofs
- Учитель: Ernesto Araya Valdivia
- Учитель: Mariia Seleznova
- Учитель: Werner Bley
- Учитель: Eva Brenner
- Учитель: Katharina Novikov
- Учитель: Julius Willing
- Учитель: Simon Gritschacher
- Учитель: Jonas Stelzig

- Учитель: Jonathan Bowden
- Учитель: Sebastian Hensel
- Учитель: Karin Binder
- Учитель: Sebastian Hensel
- Учитель: Kajetan Söhnen
Wir werden typische Aufgabenstellungen beim Staatsexamen in Analysis behandeln,
Lösungsmethoden besprechen und evtl. noch etwas zugrunde liegende Theorie
wiederholen. Wir beginnen mit dem Themenbereich
Gewöhnliche Differentialgleichungen und
arbeiten uns dann zur Funktionentheorie durch.
- Учитель: Heribert Zenk
Wir starten mit Anwendungen des Spektralsatzes wie
- stark kommutierende selbstadjungierte Operatoren
- Spektralsatz für stark kommutierende selbstadjungierte Operatoren
- stark stetige unitäre einparametrige Gruppen und deren Generatoren
- Учитель: Heribert Zenk
Mehrdimensionale Analysis -- Lehramt Gymnasium im Wintersemester 2024/2025
Dienstag 10-12 Uhr in B138 und Freitag 10-12 Uhr in B138
Beginn: Dienstag 15.10.2024
Die Vorlesung ist die dritte eines dreisemestrigen Kurses in Mathematik
für das Lehramt an Gymnasien nach der neuen Prüfungsordnung.
Einschreibung mit Schlüssel: ma
- Учитель: Fabian Darabi Far
- Учитель: Marleen Fiederer
- Учитель: Kajetan Söhnen
- Учитель: Heribert Zenk
Montag 12-14 Uhr in C123 und Donnerstag 10-12 Uhr
im Großen Physikhörsaal N120
Beginn: 14.10.2024
Die Vorlesung ist die erste eines dreisemestrigen Kurses in Mathematik
für das Physikstudium.
Am Montag 14.10. und 21.10. findet statt der Zentralübung
eine Vorlesung statt.
Einschreibung mit Schlüssel: MIP
- Учитель: Matthias Bauernfeind
- Учитель: Veronika Biber
- Учитель: Cassian Hallinger
- Учитель: Boyan Kugiyski
- Учитель: Panagiotis Papadopoulos
- Учитель: Heribert Zenk
The lecture provides an introduction to stochastic calculus with an emphasis on the mathematical concepts that are later used in the mathematical modeling of financial markets.
In the first part of the
lecture course the theory of stochastic integration with respect to
Brownian motion and Ito processes is developed. Important results such
as Girsanov's theorem and the martingale representation theorem are also
covered. The first part concludes with a chapter on the existence and
uniqueness of strong and weak solutions of stochastic differential
equations.
The second part of the lecture course gives an introduction to the arbitrage theory of financial markets in continuous time driven by Brownian motion. Key concepts are the absence of arbitrage, market completeness, and the risk neutral pricing and hedging of contingent claims. Particular attention will be given to the the Black-Scholes model and the famous Black-Scholes formula for pricing call and put options.
If you wish to participate in the course, please sign up by sending an e-mail from your LMU e-mail address to Annika Steibel (steibel@math.lmu.de).
- Учитель: Miguel Armayor Martínez
- Учитель: Julia Karczewski
- Учитель: Thilo Meyer-Brandis
- Учитель: Annika Steibel
- Учитель: Tamas Makai
- Учитель: Konstantinos Panagiotou
About this Lecture
This lecture discusses the interplay of Theory, Modelling, Numerical Methods and Implementation in Mathematical Finance.
All aspects learn from each other: one needs to understand the theory to build models and good implementations. Studying numerical experiments gives deeper theoretical insight. Using the computer to understand math can be fun!
We discuss how to build an industry-grade implementation of our models and allow future extensions while being efficient.
We discuss practical applications in the financial industry.
The lecture tries to be as self-contained as possible, but we will use some numerical methods developed in a previous course. We will start with a short recapitulation of the numerical methods needed for those who did not follow the last lecture. It is possible to consider most of these parts as “given” (“black box”). Don’t panic: We will assist you.
The lecture will discuss the theory and application of some prominent methods and models from mathematical finance. We focus on interest rate and hybrid models with high relevance for the financial industry. In an excursion, we consider a climate model (DICE), extend it and combine it with our interest rate models.
We will then use our implication to gain a deeper understanding of the theoretical properties of the model.
If time permits, we conclude the lecture by discussing running our models in a cloud.
Tentative Agenda
- Recapitulation of Numerical Methods (Monte-Carlo Method, SDEs, etc.)
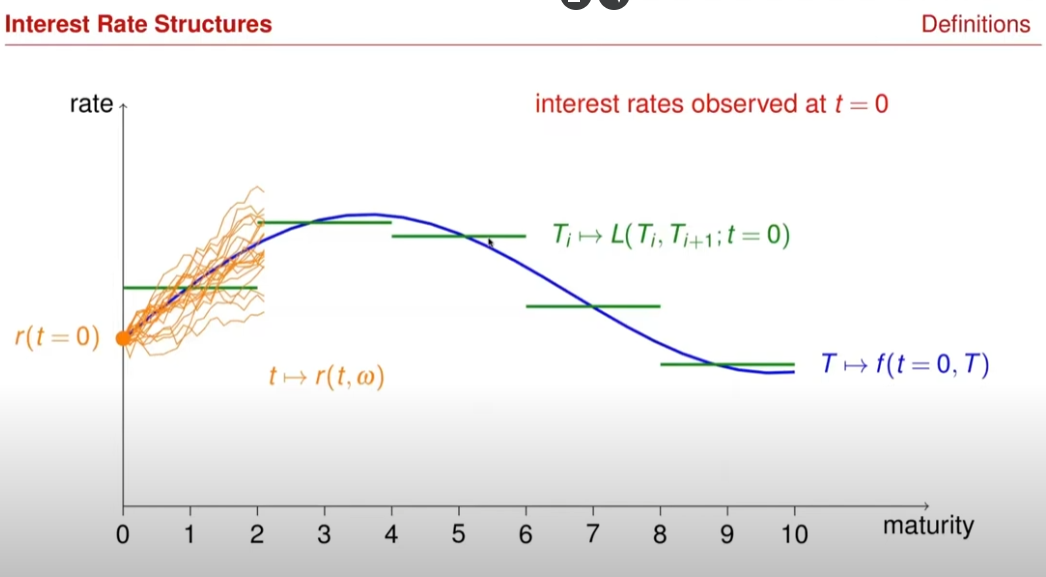
- Interest Rates, Linear Interest Rates Products
- Multiple Interes Rate Curve Modelling and its Implementation
- Interest Rate Options, Convexity Adjustment
- Discrete Term-Structure Models (formerly known as LIBOR Market Models) and their Implementation
- Model Calibration
- Valuation of Complex Derivatives
- Object Oriented Implementation, Definition of Model Interfaces
- Short Rate Models and their Implementation
- Climate Models
- Numerical Methods in the Context of Mathematical Finance
- Model Calibration: Optimization and Root-Finding
- Correlation Modelling: Prinzipal Component Analysis and Factor Reduction, Regression Methods
- IT Implementation of Models, e.g. in the Cloud
The lecture covers the object oriented implementation of the algorithms and using modern software development tools.
As part of the implementation of the models and the valuation algorithms, the lecture will discuss some of the latest standards in software development.
- revision control systems (git)
- unit-testing (junit)
- build management (maven, gradle)
- continuous integration (TravisCI, Jenkins)
Implementation will be performed in Java (Eclipse, IntelliJ)
- Учитель: Christian Fries
- Учитель: Niklas Weber
Course Description
In this reading course, we will study stochastic processes in continuous time that happen to be sub- or supermartingales. In particular, this includes martingales. After proving Doob's maximal inequalities and stopping theorem, we will derive the quadratic variation of a local martingale. As a result, we will be able to understand the notion of a semimartingale.
Target Participants
- Master students of Mathematics
Pre-requisites
- Probability theory and measure and integration theory
- Учитель: Alexander Kalinin
Course Description
In this seminar, we will analyse one-dimensional stochastic differential equations (SDEs) driven by a Brownian motion. To this end, a short review of semimartingales, stochastic integrals and Itô's formula will be discussed. Under Lipschitz conditions on the drift and diffusion coefficients of the SDE, we will derive unique strong solutions. In particular, we will recover the Brownian bridge, the geometric Brownian motion and the Ornstein-Uhlenbeck process as solutions of affine SDEs.
Target Participants
- Master students of Mathematics and Financial and Insurance Mathematics
Pre-requisites
- Probability theory and measure and integration theory
- Учитель: Alexander Kalinin
Course Description
In this lecture, we will consider various classes of stochastic processes that may differ in their state spaces and underlying index sets with a special focus on Gaussian, Lévy and Markov processes. In summary, the lecture will be divided into three core topics: the construction, the path behaviour and the probabilistic analysis of general stochastic processes.
Target Participants
- Master students of Mathematics and Financial and Insurance Mathematics
Pre-requisites
- Probability theory and measure and integration theory
- Учитель: Alexander Kalinin
- Учитель: Wiebke Bartolomaeus
- Учитель: Paula Reichert-Schürmer
- Учитель: Paula Reichert-Schürmer
- Учитель: Anna Ribelles Perez
- Учитель: Thomas Sørensen
- Учитель: Adalbert Fono
- Учитель: Gitta Kutyniok
Einschreibeschlüssel: Newton24/25
- Учитель: Rupert Frank
- Учитель: Jonas Peteranderl
- Учитель: Paul Pfeiffer
- Учитель: Karl-Wilhelm Georg Bollweg
- Учитель: Katharina Oberpriller
Einschreibeschlüssel: Diff1WS24
- Учитель: Daniel Rost
- Учитель: Tizian Wenzel
Einschreibeschlüssel: LA1WS24
- Учитель: Lukas Böke
- Учитель: Laura Paul
- Учитель: Daniel Rost
Einschreibeschlüssel: Querschnitt24W
- Учитель: Erwin Schörner
- Учитель: Leonard Wetzel
Einschreibeschlüssel: Grundlagen1W24
- Учитель: Stefan Kolek Martinez De Azagra
- Учитель: Stefan Kolek Martinez de Azagra
- Учитель: Erwin Schörner
Einschreibeschlüssel: ExamUF24W
- Учитель: Daniel Rost
- Учитель: Erwin Schörner
Blockkurs in der vorlesungsfreien Zeit, in dem die Grundlagen des
Textsatzsystems LaTeX und speziell die Erstellung mathematischer Texte
behandelt werden. Nähere Informationen zu Ablauf und Anmeldung auf der Webseite des Kurses.
- Учитель: Mechtild Callies
Enrolment key: ICV
- Учитель: Emanuela Giacomelli
- Учитель: Markus Land
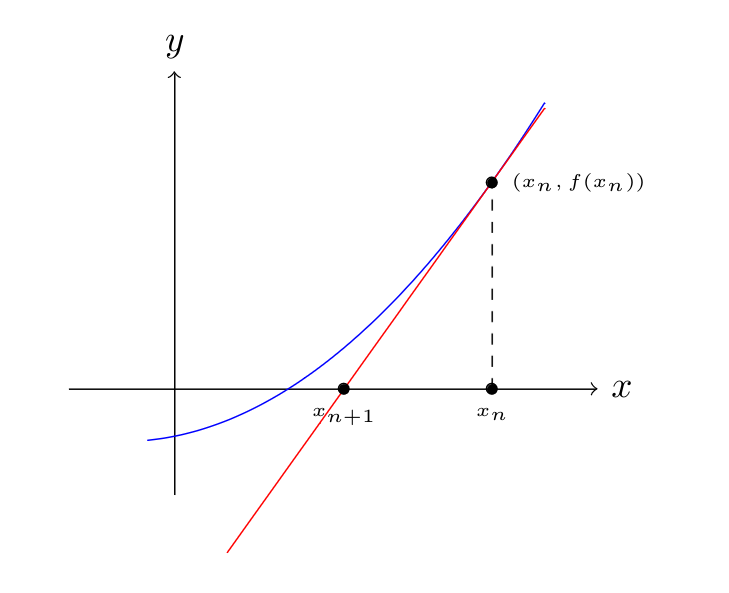
Inhalt der Vorlesung ist eine Einführung in die Optimierung in - vornehmlich - endlicher Dimension. Wichtige Themen und Inhalte sind unter anderem:
Konvexität, Lineare Programme und ihre Standardformen, Existenz von Lösungen für lineare Programme, Dualitätstheorie für lineare Programme, das Simplexverfahren, Formulierung und Existenz von Lösungen konvexer Optimierungsprobleme, duale Darstellung konvexer Funktionen und die Kuhn-Tucker-Theorie.
- Учитель: Julian Becker
- Учитель: Konstantinos Panagiotou
Wir beginnen mit einer Einführung in die klassische Algebraische Geometrie der affinen und projektiven Varietäten und deren Morphismen. Zu den weiteren Themen gehören rationale Abbildungen, Dimension, Vollständigkeit, Tangentialräume, singuläre Punkte, Normalisierung und Aufblasungen.
Im Anschluss geben wir eine Einführung in die Theorie der Garben und Schemata.
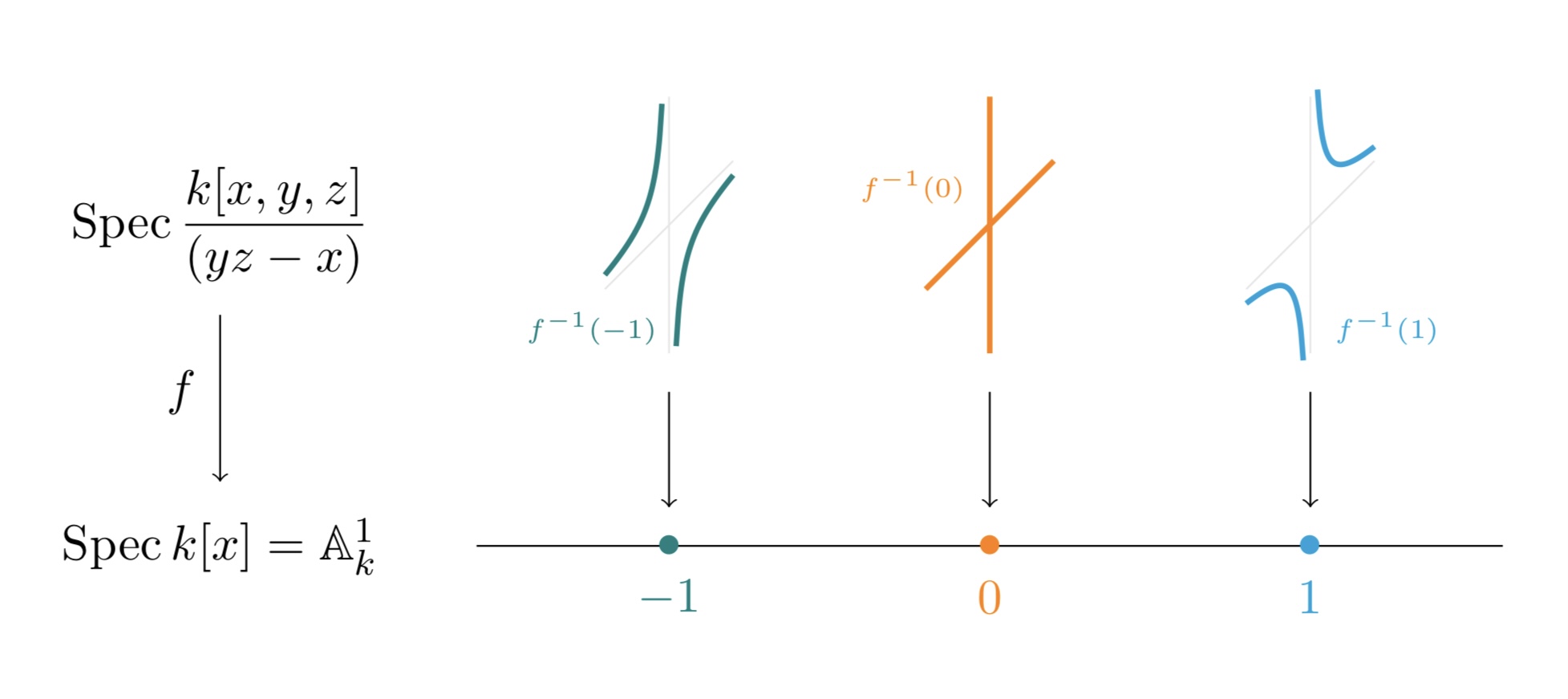
- Учитель: Andreas Rosenschon
- Учитель: Simon Seidenschwarz
- Учитель: Jonas Beyrer
- Учитель: Christian Lange
- Учитель: Bernhard Leeb
Passwort: cantelli
- Учитель: Sabine Jansen
- Учитель: Fabian Nolte
Einschreibung öffnet am 7. Oktober 2024.
Klausuranmeldung (in 2025) ausschließlich über Moodle.
- Учитель: Leon Bollmann
- Учитель: Maximilian Duell
- Учитель: Thomas Sørensen
